童年如作业的博客

天 生 我 材 必 有 用 ，
千 金 散 尽 还 复 来 。

分数化小数

发表于 分类于 ，
阅读次数： Valine：
本文字数： 2.7k 阅读时长 ≈ 2 分钟

[USACO2.4]Fractions to Decimals【分数化小数】

PS: 一道经典的模拟题（或许以后高精会用上），需要用到数学的基本知识（如何判断循环节）

题意简述

给你分数的分子 $N$ 和分母 $D$ ，求 $\frac{N}{D}$ 的分值。如果分值是整数，保留一位小数。如果分值是循环小数，用小括号 $()$ 括住循环节。如果答案长度超过 $76$ ，每行输出 $76$ 个字符后换行。

题目分析

注意：N/D是分数，分数属于有理数，有理数分为整数、有限小数和无限循环小数

这道题让你算的 $\frac{N}{D}$ 的值会有多种情况：

  1. $N$ 可以被 $D$ 整除（即 $N \div D$ 的值是一个整数），但输出需在末尾加上 $.0$ ，例如 $2 \div 2 = 1.0$ 。
  2. $N$ 可以被 $D$ 除尽（即 $N \div D$ 的值是一个有限小数），例如 $55 \div 100 = 0.55$ 。
  3. $N$ 不可以被 $D$ 除尽（即 $N \div D$ 的值是一个无限循环小数），循环节用一对小括号 $()$ 括住，例如 $1 \div 3=0.(3)$ （所以想用double的同学请绕道吧，无限小数是会爆精的）。

算法

模拟

算法解析

由于用double会爆精，我们只好进行手动的除法模拟。经过 $\color{purple}RE$ 的手动验证，我发现有些答案的长度超过了$10^{7}$ ，所以不能用数组模拟，因为$int$类型数组开$10^{8}$会爆空间 $(MLE)$ 。所以我们得用字符串模拟除法（因为字符串是无限空间的）。

  • 首先，答案的整数部分可以直接通过 $N/D$ 算出，所以我们可以直接把字符串赋值为 $N/D$ 的值，然后再加一个小数点$(.)$，因为答案无论如何都有小数部分。

  • 然后，就是最重要的除法模拟部分了。本题模拟的核心思路正是除法笔算（长这样的）

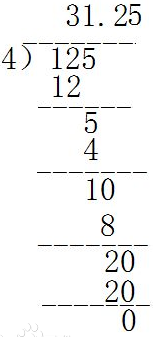
    由图可知，算商的小数部分时，会将上一次除下来的余数后面加上被除数的对应位的数字（如果没有就视作0）作为被除数，继续做除法。

    现在，模拟思想问题已经解决了，但如何判断循环节又成了一道难关。因为小数部分的商与前面相同时也不一定是循环节， $555 \div 1000 = 0.555$ 就是一个经典的例子，它其实是一个有限小数，所以排除了用商作为判断条件的可能性。

    有没有其他东西可以作为循环节的判断条件呢？答案是有的。通过观察我们发现，即使除出来的的商相同，商不是循环节的对应被除数（之前的余数）前面是找不到的，也就是循环节的数具有被除数相同的必然性。例如 $1 \div 3=0.3333……$ ，小数部分是这样的出来的：

    如图，循环节 $3$ 的被除数一直是 $10$ ，也就是之前算的余数一直是 $1$ ，余数相同。所以我们只要标记出现过的余数，如果有余数与之前的相同，那么之前余数作为被除数算出的商的位置直到算出这个余数的商的位置就是这个小数的循环节！

    解决了循环节的判断问题后，剩下的就简单了。

  • 最后，就是输出了。输出也没什么难的，但要注意 $76$ 个字符换一行，不要忘记记上整数部分、小数点和小括号。

程序

1
备注：do{}while()是先执行一次{}里的程序后，再进行判断符不符合()里的条件而决定是否继续循环的循环语句。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<iostream>
#include<fstream>
#include<cstdio>
#include<algorithm> 
#include<string>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
int n,d,k,w,sum,len;
//w用来记录循环节开始（左括号）的位置，sum为输出使用的计数器 
string ans;
//答案 
int pd[100005];
//pd数组用来记录每个余数出现的位置，判断余数是否重复，便于记录循环节开始（左括号）的位置。根据题目1<=N,D<=100000可得知余数最终不会超过99999 
int main()
{
     
    scanf("%d%d",&n,&d);
    k=n/d,w=-1;
    do
    {
        ans=char(k%10+'0')+ans;
		//这种方法要把拆分出来的整数放到前面去，不然会反过来，因为它先拆分个位，再拆分十位，直接加会使个位在前，直接加会使十位在后， 
        k/=10;
    }while(k>0);
	//拆分结果的整数部分进ans。由于0也算是整数部分，所以无论如何也要拆分一次，用do{}while()，不然用for() 整数部分为0时就不会拆进去，因为k=0了 
    ans+='.';
	//鉴于结果无论如何至少有一位小数，加个小数点
    n=n%d;
	//被除数取余，开始模拟小数部分的除法运算 
    do
    {
        if(pd[n]!=0)
        {
            w=pd[n];
            break;
        }
		//如果余数有重复，说明这是一个循环小数，上一个n出现的位置便是循环节开始（左括号）的位置
        else pd[n]=ans.size();
		//否则就记下这个余数变为被除数后对应的商出现的位置，以便未来判断和记录 
        n*=10;
		//n变成被除数，末尾加0（N,D一定是正整数，不存在小数可加在末尾）
        k=n/d;
        ans+=char(k+'0');
        n=n%d;
		//模拟除法 
    }while(n!=0);
	//由于结果如果是正整数的话，末尾也得加0，用do()while{} 
    if(w!=-1) ans+=')';
	//如果结果是一个循环小数，在末尾加个右括号，便于输出 
    len=ans.size();
    for(int i=0;i<len;i++)
    {
        if(i==w)
        {
            putchar('(');
            i--;
            w=-1;
        }
        //如果这个地方是循环节的开头，在这里输出左括号，并将w改为-1，避免重复输出括号，同时i--，因为这里的ans[i]还没输出  
        else putchar(ans[i]);
        sum++;
        if(sum%76==0) putchar('\n');
		//putchar( )可理解为cout<<char( );
    }
    //注：我这样处理循环节的开头是为了便于换行，因为左括号也算是字符 
    return 0;
}
Title - Artist
0:00